
De aarde is rond
Data, data en nog eens data. Met lange en ingewikkelde getallenreeksen kunnen de meeste mensen niet uit de voeten. Een patroon is er nauwelijks in te ontdekken. Totdat je gaat visualiseren. Een kaart, grafiek of infographic geeft ineens inzicht. Onlangs publiceerde het PBL het jubileumboek ‘Kennis verbeeld: lessen uit 25 jaar datavisualisatie voor beleid’. In een serie blogs presenteert het PBL-visualisatieteam de komende weken een aantal van de geleerde lessen. In deze blog gaat Jan de Ruiter in op de uitdagingen bij het weergeven van een bol op een plat vlak.
De beperkingen van het platte vlak
We maken voor onze publicaties vaak kaarten van Nederland, Europa of de wereld, maar al deze kaarten zijn fout. Het is onmogelijk om een boloppervlak zonder vertekeningen op een plat vlak over te zetten. Welke projectiemethode je ook kiest, hoeken, afstanden of vormen kloppen niet. Ook voor regionale kaarten moet je corrigeren voor de bolling van het oppervlak, al is dat effect kleiner en minder goed te zien dan op een wereldkaart. In alle gevallen geldt dat je niet zomaar een projectie kunt kiezen.

De Mercatorkaart
De bekendste wereldkaart is de Mercatorkaart. Het grootste nadeel van deze kaart is dat gebieden groter worden weergegeven naarmate ze verder van de evenaar af liggen. In werkelijkheid zijn Groenland en Saoedi-Arabië ongeveer even groot, maar op de Mercatorkaart is Groenland zelfs groter dan heel Afrika! Toch wordt deze kaart veel gebruikt bij online kaarten (bijvoorbeeld Google Maps), omdat de vormen en hoeken behouden blijven. Google Maps wordt vooral gebruikt op lokale schaal en dan is het belangrijk dat rechte hoeken niet vervormen. Door slimme algoritmes te gebruiken en de schaalbalk aan te passen aan de breedtegraad waarop is ingezoomd, is afstandsbepaling mogelijk. Bij uitzoomen naar mondiale schaal worden de afwijkingen echter zo groot dat je beter een andere projectie kunt kiezen.
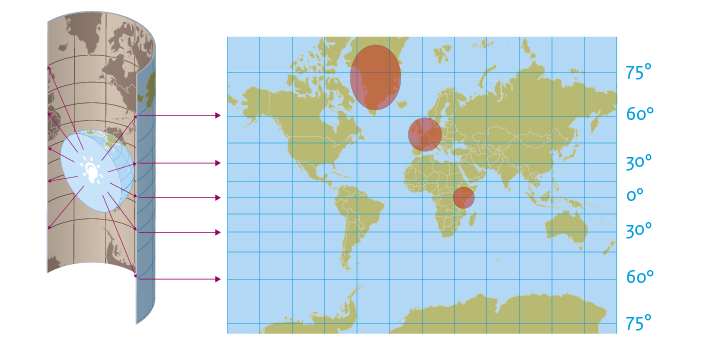
Wereldkaarten voor grids: lat/lon-projectie
Bij berekeningen wordt vaak gebruikgemaakt van de ‘equirectangular’ of rechthoekige projectie, ook wel lat/lon-projectie genoemd (van latitude-longitude). De lengte- en breedtegraden worden gebruikt als x- en y-coördinaten in een plat vlak. Daarmee wordt elk gebied van één bij één graad een vierkant van gelijk oppervlak, waardoor de wereld kan worden afgebeeld als een rechthoekig grid. Omdat wordt gerekend met vierkante gridcellen is herprojectie tijdens berekeningen niet nodig. De afwijkingen in vorm en oppervlakte op hogere en lagere breedtegraden zijn echter groot. Om die reden gebruiken we deze projectie liever niet in het eindbeeld. De rode ellipsen in de kaart hiernaast zouden op de wereldbol cirkels zijn met een gelijk oppervlak.
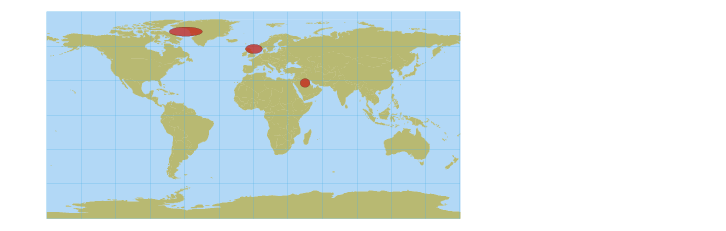
Oppervlaktegetrouwheid
Voor het objectief weergeven van de verspreiding van verschijnselen over de aardbol is oppervlaktegetrouwheid erg belangrijk. De Mercatorprojectie is met haar enorme oppervlaktevervormingen daarvoor bijzonder ongeschikt. Er bestaan projecties die wel min of meer oppervlaktegetrouw zijn (Mollweide, Goode, Gall-Peters), maar het gevolg van deze keus is dat afwijkingen in hoeken en vormen groot zijn.

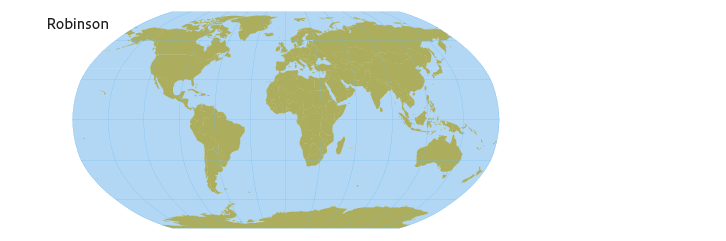
Projectie wereldkaart bij het PBL
Bij het PBL gebruiken we de zogeheten Robinsonprojectie voor het maken van wereldkaarten. Deze projectie levert een visueel aantrekkelijk beeld op waarbij een compromis is gesloten tussen afwijkingen van vorm, afstanden en oppervlak. Bijzonder is dat de Amerikaanse cartograaf Robinson in 1963 eerst het gewenste kaartbeeld bedacht en vervolgens bij dat beeld de benodigde rekenkundige factoren bepaalde. Bij de meeste projecties is het andersom, die gaan uit van wiskundige formules op basis waarvan een kaartbeeld berekend wordt.
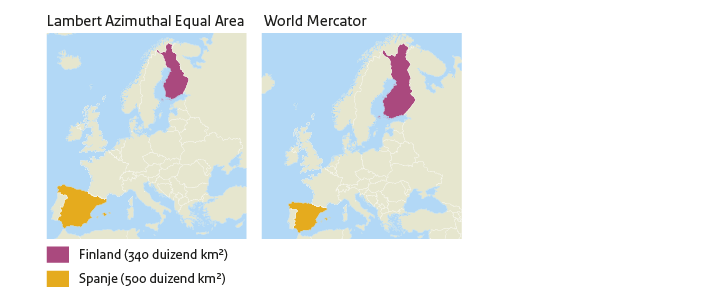
Europa
Voor kaarten van Europa gebruiken we een oppervlaktegetrouwe projectie die het European Environment Agency (EEA) aanbeveelt, de Lambert Azimuthal Equal Area. In de kaartjes hieronder vergelijken we de oppervlaktes van Finland en Spanje in deze projectie met die in de Mercatorprojectie. Het is duidelijk te zien dat oppervlaktes in de Mercatorprojectie ook op Europese schaal in de noordelijke landen worden overschat.
Nederland
Voor Nederland hanteren we een projectie met nauwelijks vervorming (RD New). Bij deze projectie is de vertekening gering, in afstand tussen -10 en +18 centimeter per kilometer. In de kaartjes hiernaast projecteren we Nederland in RD New en Lat/Lon. In de Lat/Lon-projectie zijn zowel de vormen als de afstanden erg vertekend.
