Planbureau voor de Leefomgeving
Toon filters
Filter op periode

Dat is lastig schatten

Blog

Data, data en nog eens data. Met lange en ingewikkelde getallenreeksen kunnen de meeste mensen niet uit de voeten. Een patroon is er nauwelijks in te ontdekken. Totdat je gaat visualiseren. Een kaart, grafiek of infographic geeft ineens inzicht. Onlangs publiceerde het PBL het jubileumboek ‘Kennis verbeeld: lessen uit 25 jaar datavisualisatie voor beleid’. In een serie blogs presenteert het PBL-visualisatieteam de komende weken een aantal van de geleerde lessen. In deze blog gaat Allard Warrink in op hoe verschillend de grootte van cirkels door lezers ingeschat wordt.

Cartoon met persoon die zegt: “Wow! De maan is vandaag echt groot!” terwijl deze kijkt naar de maan die laag aan de horizon staat
De maan is altijd even groot, toch lijkt ze hoog aan de hemel veel kleiner dan laag aan de horizon

Hoe je met cirkels een betrouwbaar beeld geeft

Iedereen kent ze wel, kaarten met cirkels. Handig om hoeveelheden en hun verschillen weer te geven. Cirkels zijn goed intuïtief te begrijpen: hoe groter de cirkel, hoe groter de afgebeelde waarde. Ze zijn ook erg geschikt om data met een groot bereik af te beelden. Dat komt omdat je eigenlijk de hoeveelheid over twee dimensies verdeelt: het oppervlak neemt kwadratisch toe. Een ander voordeel van cirkels is dat ze zeer geschikt zijn om geografische spreiding mee aan te geven. Dat kan omdat je onafhankelijk van de cirkelgrootte altijd een duidelijk midden kunt aanwijzen en dus het punt op de kaart waarvan het de waarde afbeeldt. Dit in tegenstelling tot bijvoorbeeld een staaf met een variërende lengte, daarvan is niet direct duidelijk hoe deze is geplaatst op de kaart. Bij het begin, het midden of een andere plek van de staaf?

Er zijn ook nadelen. Als je veel data moet afbeelden of als de geografische spreiding erg geclusterd is, kunnen cirkels elkaar gaan overlappen of zelfs helemaal bedekken. En kun je niet meer goed lezen wat er staat. Ook is het lastig om het verschil in oppervlak van cirkels met verschillende grootte goed in te schatten. We weten dat een lezer het oppervlak van een grote cirkel vaak te klein inschat. Er zijn verschillende methodes om dit probleem op te lossen die allemaal weer eigen voor- en nadelen hebben. Belangrijk is in ieder geval dat de cirkel of een vervangend symbool qua grootte een direct verband moet houden met de waarde die hij voorstelt.

Straal is geen schaal

Een fout die soms gemaakt wordt bij het ontwerpen van cirkels, is dat de af te beelden waarde niet gekoppeld is aan het oppervlak, maar aan de straal van de cirkel. In dat geval neemt het oppervlak exponentieel toe met de waarde. Dit leidt bij een grote spreiding van de waarden tot extreme afwijkingen.

Twee groepen van cirkels. De eerste met een straal gelijk aan de waarde, de tweede met het oppervlak gelijk aan de waarde. De laatste groep geeft een beter beeld van de waarde.
Als de waarde niet omgerekend wordt naar oppervlak maar als straal gebruikt wordt ontstaat een verkeerd beeld

Ogenschijnlijk kleiner

Hoe groter een cirkel, hoe meer de oppervlakte wordt onderschat ten opzichte van kleinere cirkels. De oppervlakte van de buitenste cirkel hieronder is twee keer zo groot als die van de binnenste cirkel. Toch zullen de meeste mensen de inschatting maken dat de buitenste cirkel veel minder dan twee keer zo groot is.

Twee concentrische cirkels
Het oppervlak van de buitenste ring lijkt kleiner dan het oppervlak van de binnenste cirkel

Optisch bedrog

Hoe je de grootte van een cirkel inschat, wordt beïnvloed door de cirkels in de omgeving. In het voorbeeld hieronder zijn de cirkels in het midden precies even groot. Toch zullen de meeste mensen de blauwe cirkel links kleiner inschatten.

Twee cirkels van gelijke grootte. De linker omgeven door grote cirkels, de rechter door kleine cirkels
De linker blauwe cirkel lijkt kleiner dan de rechter

Hulp bij en alternatieven voor cirkels

Een eenvoudig hulpmiddel bij het inschatten van de cirkeloppervlakten is om de waarden te vermelden naast de cirkels. Dit werkt bij kaarten met niet te veel gegevens én op voorwaarde dat voor de lezer duidelijk is dat de waarden bij de cirkels horen.

: Kaart van de wereld met cirkels van verschillende grootte daarin. Naast de cirkels labels met de waarde.
Labels met de waarde helpen bij het inschatten

Een andere mogelijkheid is om de cirkels te vervangen door kleine staafdiagrammen. De meeste mensen kunnen verschillen in lengte beter inschatten dan verschillen in oppervlakte. Een nadeel is wel dat staafdiagrammen die hoge waardes weergeven al snel buiten het gebied waar ze over gaan getekend moeten worden.

Kaart van de wereld met staven van verschillende grootte daarin
De lengte van een staafje is beter in te schatten dan het oppervlak van een cirkel

Een derde mogelijkheid is het weergeven van de gegevens met symbolen die staan voor een bepaalde hoeveelheid. Deze kun je eenvoudig tellen als lezer. Verschillen komen zo duidelijker naar voren en de weergave blijft compact.

Kaart van de wereld verschillende aantallen blokjes daarin
Door blokjes te gebruiken kunnen de waarden eenvoudig geteld worden

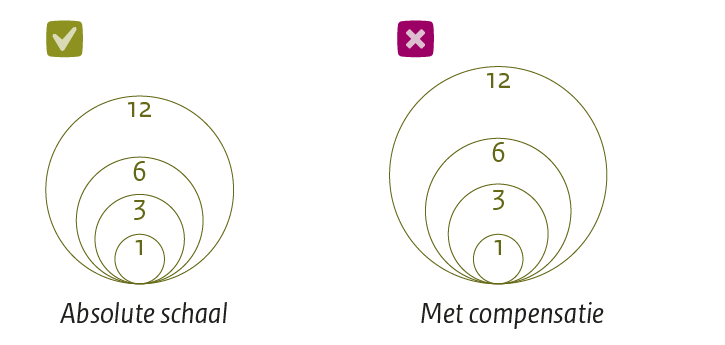
Compenseren?

Al in de jaren 20 van de vorige eeuw werd onderzoek gedaan naar hoe mensen cirkels inschatten. In 1956 ontwikkelde de geograaf James Flannery een methode om de grootte van cirkels aan te passen zodat het afgebeelde oppervlak beter werd ingeschat. Het grote nadeel van deze methode is dat het oppervlak van de cirkels in de figuur niet meer direct correspondeert met de afgebeelde data. Dit kan tot verkeerde inschattingen leiden en als een lezer de cirkels zou opmeten, levert dit foute resultaten op. Bij het PBL verbeelden we de data in cirkels daarom altijd exact proportioneel.

Twee groepen met concentrische cirkels. De linker groep is niet gecompenseerd, de rechter groep wel.
Compenseren voor het de gemiddelde inschattingsfout is niet aan te raden omdat de grootte van de cirkel dan niet meer direct correspondeert met de data